外观
矩阵
约 15933 字大约 53 分钟
高级
注意
本页面包含高级内容。如果您是 Mine Script® 编程初学者,建议先熟悉其他更基础的 Mine Script 功能,再学习本部分内容。
简介
Mine Script矩阵是以矩形格式存储值引用的集合。它们等同于具有检查、修改和专门计算功能的二维数组对象。与数组类似,矩阵的所有元素必须是相同类型、用户自定义类型或枚举类型。
矩阵使用两个索引来引用其元素:一个索引对应行,另一个对应列。每个索引从0开始,最大值为矩阵行数/列数减一。Mine中的矩阵可以具有动态变化的行数和列数(随K线变化而变化)。矩阵中的元素总数是行数和列数的乘积(例如,5x5矩阵共有25个元素)。与数组相同,矩阵中元素总数不得超过100,000。
矩阵声明
Mine Script 采用以下语法声明矩阵:
[var/varip ][matrix<type> ]<identifier> = <expression>其中 <type> 是用于声明矩阵值类型的类型模板,<expression> 返回该类型的矩阵实例或 na。
当将矩阵变量声明为 na 时,用户必须通过包含 matrix 关键字后跟类型模板来指定该标识符将引用特定类型的矩阵。
以下代码声明了一个值为 na 的新变量 myMatrix。它明确将变量声明为 matrix<float>,这向编译器表明该变量只能接受包含浮点值的矩阵对象:
Mine Script®
已复制
当矩阵变量未被赋值为 na 时,matrix 关键字及其类型模板可省略,因为编译器将从变量引用的对象中获取类型信息。
在此示例中,我们声明了一个 myMatrix 变量,它引用一个新的 matrix<float> 实例(包含两行、两列,初始值为 0)。这种情况下变量从新对象获取类型信息,因此不需要显式类型声明:
Mine Script®
已复制
使用 var 和 varip 关键字
与其他变量类似,用户可以使用 var 或 varip 关键字指示脚本仅声明一次矩阵变量(而非每根K线都重新声明)。以此方式声明的矩阵变量将始终指向同一实例(除非脚本显式分配其他矩阵),使得矩阵及其元素引用能在脚本迭代间持续存在。
以下脚本使用 var 关键字声明矩阵变量 m,该矩阵包含单行两个整型元素。每20根K线,脚本会给矩阵 m 第一行的第一个元素加1。通过 plot() 调用在图表上显示该元素值。如图所示,m.get(0, 0) 的值在K线间持续存在,不会回到初始值0:
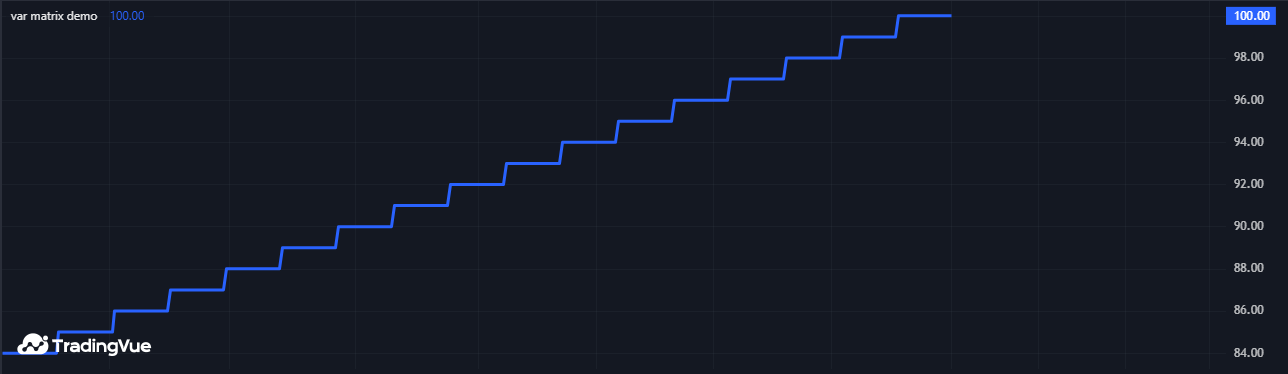
Mine Script®
已复制
注意
使用 varip 声明的矩阵变量在历史数据上的行为与 var 相同,但在实时 K 线(即脚本最后一次编译后出现的 K 线)上,会在每次价格变动时更新其值。通过 varip 声明的矩阵变量仅可包含 int、float、bool、color 或 string 类型,或者字段仅包含这些类型或其集合(数组、矩阵和映射)的用户自定义类型。
矩阵元素读写
matrix.get() 和 matrix.set()
要从矩阵中指定行和列索引处获取值,请使用 matrix.get()。此函数会定位指定的矩阵元素并返回其值。同样地,要覆盖特定元素的值,请使用 matrix.set() 将指定行和列的元素赋为新值。
以下示例在第一根K线定义了一个两行两列的方阵 m,所有元素的初始值为 0。脚本在不同K线上使用 m.get() 和 m.set() 方法为每个元素的值加 1:第一行第一个值每 11 根K线更新一次,第一行第二个值每 7 根K线更新一次,第二行第一个值每 5 根K线更新一次,第二行第二个值每 3 根K线更新一次。脚本在图表上绘制每个元素的值:
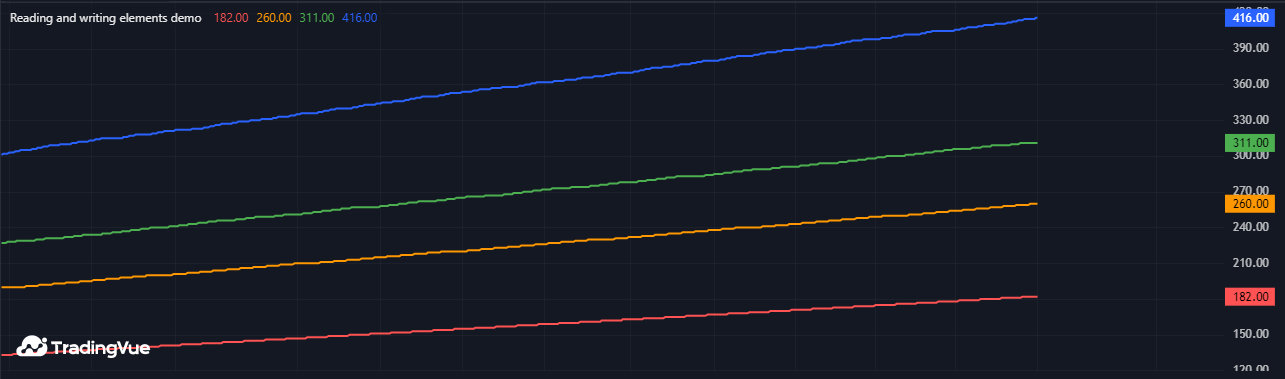
Mine Script®
已复制
matrix.fill()
使用 matrix.fill() 可将矩阵中所有元素覆盖为指定值。该函数会将整个矩阵或指定行/列索引范围内的所有元素设置为调用时指定的值。例如,以下代码片段声明了一个4×4方阵,然后使用随机值填充其元素:
Mine Script®
已复制
使用 matrix.fill() 填充包含特殊类型( 线(line)、线填充(linefill)、方框(box)、多段线(polyline)、标签(label)、表格(table) 和 图表点(chart.point) )或用户自定义类型(UDT)的矩阵时需注意:所有被替换元素将指向函数调用中传入的同一个对象。
以下脚本声明了一个4行4列的标签引用矩阵,并在第一根K线用新标签对象填充。每根K线上,脚本会将第0行第0列引用的标签的x属性设置为bar_index,并将第3行第3列引用的标签的text属性设置为图表上的标签数量。虽然该矩阵可引用16个(4x4)标签,但每个元素都指向同一实例,导致图表上仅显示一个标签(其x和text属性会在每根K线更新):

Mine Script®
已复制
矩阵的行与列
检索
矩阵通过matrix.row()和matrix.col()函数便于检索特定行或列的所有值。这些函数将值作为数组对象返回,数组大小根据矩阵的另一维度确定,即matrix.row()数组的大小等于列数,matrix.col()数组的大小等于行数。
以下脚本在第一根图表K线上用值1-6填充一个3x2的m矩阵。它调用m.row()和m.col()方法从矩阵中访问第一行和第一列数组,并将它们与数组大小一起显示在图表上的标签中:
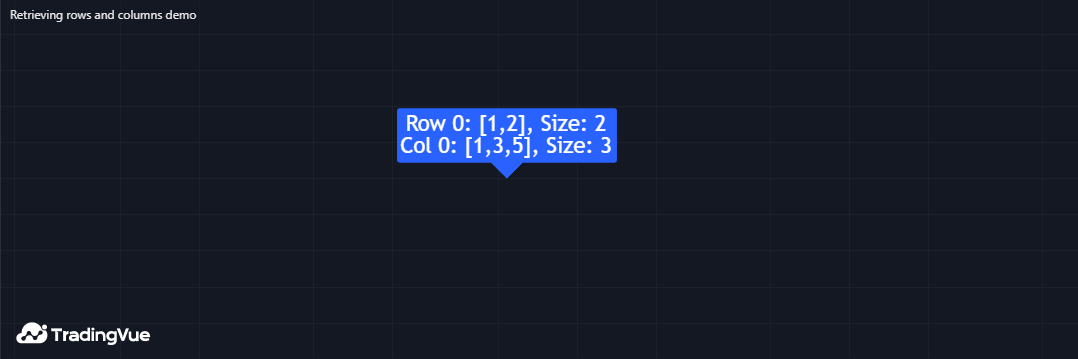
Mine Script®
已复制
请注意:
- 为了获取标签中显示的数组大小,我们使用了rows()和columns()方法而非array.size(),以此演示
row0数组的大小等于列数,而column0数组的大小等于行数。
matrix.row()和matrix.col() 会将行/列中的引用复制到新数组中。对这些函数返回的数组进行修改不会直接影响矩阵元素或矩阵形状。
在此我们修改了之前的脚本,在显示标签前通过array.set()方法将row0的第一个元素设为10。该脚本同时绘制第0行第0列的值。如我们所见,标签显示row0数组的第一个元素为10,但图表显示对应矩阵元素值仍为1:
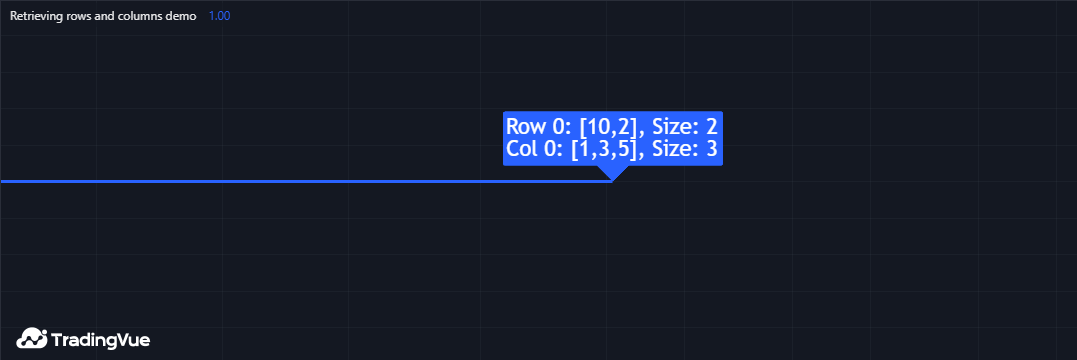
Mine Script®
已复制
虽然对matrix.row()或matrix.col() 返回数组的修改不会直接影响父矩阵,但需特别注意:当矩阵包含用户自定义类型(UDT)或特殊类型(包括线(line)、线填充(linefill)、方框(box)、多段线(polyline)、标签(label)、表格(table) 和 图表点(chart.point))时,这些函数返回的数组是行/列的浅拷贝,即数组中的元素与对应矩阵元素指向相同的对象。
以下脚本定义了一个包含初始值为0的value字段的自定义类型myUDT。它在第一根K线声明了1x1矩阵m来保存单个myUDT实例,然后调用m.row(0)将矩阵第一行复制为数组。每根K线上,脚本会给第一行数组元素的value字段加1。此时矩阵元素的value字段也会随之增加,因为两者引用的是同一个对象:
Mine Script®
已复制
插入
脚本可以通过 matrix.add_row()和matrix.add_col() 向矩阵添加新行和列。这些函数将数组中的值引用插入到矩阵的指定行/列索引位置。如果目标矩阵 id 为空(没有行或列),调用时使用的 array_id 可以是任意大小。如果在指定索引位置已存在行/列,矩阵会将该索引及之后所有现有行/列的索引值增加1。
以下脚本声明了一个空矩阵 m,并使用 m.add_row() 和 m.add_col() 方法插入行和列。它首先在行0插入一个包含3个元素的数组,将 m 转为1×3矩阵,然后在行1插入另一个数组,将矩阵变为2×3。接着在行0再次插入数组,将矩阵变为3×3,并将原索引0及以上的所有行索引后移。随后在最后一列索引处插入数组,将矩阵变为3×4。最后在末尾行索引处添加包含4个值的数组。
最终生成的矩阵为4×4,包含按升序排列的值1-16。脚本使用自定义的 debugLabel() 函数在每次行/列插入后显示 m 的行数据,以可视化整个过程:

Mine Script®
已复制
注意
正如从包含线(line)、线填充(linefill)、方框(box)、多段线(polyline)、标签(label)、表格(table) 和 图表点(chart.point)或用户自定义类型(UDT)实例的矩阵中获取的行或列数组是浅拷贝一样,包含这些类型的矩阵元素与插入其中的数组引用的是相同的对象。在这种情况下,对任一对象中元素值的修改都会影响另一个对象。
移除
要从矩阵中移除特定行或列,请使用 matrix.remove_row() 和 matrix.remove_col()。这些函数会移除指定的行/列,并将其后所有行/列的索引值减1。
在本示例中,我们在前文"行与列演示"脚本的基础上添加了以下代码:
Mine Script®
已复制
这段代码使用 m.remove_row() 和 m.remove_col() 方法移除了矩阵 m 的第一行和最后一列,并在 bar_index + 30 处用标签显示剩余行。如我们所见,执行此代码块后 m 变为 3x3 形状,且所有现有行的索引值都减1:

交换
要交换矩阵的行和列而不改变其维度,请使用 matrix.swap_rows() 和 matrix.swap_columns()。这些函数会交换位于 row1/column1 和 row2/column2 索引处的元素位置。
我们在前例中添加以下代码,交换 m 的第一行和最后一行,并在 bar_index + 40 处用标签显示变化:
Mine Script®
已复制
在新标签中,我们可以看到矩阵的行数与之前相同,且第一行和最后一行已完成位置交换:

替换
在某些情况下,可能需要完全替换矩阵中的某一行或列。为此,可以在所需行/列处插入新数组,并移除该索引处原有的元素。
在以下代码中,我们定义了一个 replaceRow() 方法,该方法使用 add_row() 在行索引处插入新值,并使用 remove_row() 移除已移动到 row + 1 索引处的旧行。此脚本使用 replaceRow() 方法用数字1-9填充一个3×3矩阵的行。它通过自定义的 debugLabel() 方法在替换行前后在图表上绘制标签:

Mine Script®
已复制
遍历矩阵
for
当脚本只需遍历矩阵的行/列索引时,最常用的方法是使用 for 循环。例如,以下代码创建一个循环,row 值从0开始,每次增加1,直到达到矩阵 m 的行数减1(即最后一行索引):
Mine Script®
已复制
要遍历矩阵 m 中的所有索引值,我们可以创建一个嵌套循环,在每个行值上迭代遍历各列索引:
Mine Script®
已复制
让我们使用这种嵌套结构创建一个可视化矩阵元素的方法。在以下脚本中,我们定义了 toTable() 方法,该方法在表格(table)对象中显示矩阵元素。它遍历每个行索引及每行的列索引,在循环中将每个元素转换为字符串显示在对应的表格单元格中。
在第一根K线上,脚本创建一个空矩阵 m,填充行数据,并调用 m.toTable() 显示其元素:

Mine Script®
已复制
for...in
当脚本需要遍历并获取矩阵的行时,相比标准for循环,使用for...in结构通常是更优选择。该结构直接引用矩阵中的行数组,为此类用例提供了更便捷的操作方式。例如,以下代码创建了一个循环,为矩阵m中的每一行返回对应的行数组:
Mine Script®
已复制
以下指标计算OHLC数据的移动平均(使用输入长度设置)并将结果显示在图表上。自定义的 rowWiseAvg() 方法通过 for...in 结构遍历矩阵行,生成包含每行 array.avg() 结果的数组。
在首根K线上,脚本创建一个包含4行(对应OHLC)和长度参数指定列数的新矩阵 m,随后在每根K线通过 m.add_col() 和 m.remove_col() 方法队列式更新OHLC数据列。脚本使用 m.rowWiseAvg() 计算各行平均值数组,并将元素值绘制在图表上:
Mine Script®
已复制
请注意:
for...in循环也可以引用每行的索引值。例如,for [i, row] in m会在每次循环迭代时创建一个包含行索引i和对应行数组row的元组:
矩阵复制
浅拷贝
Mine脚本可通过matrix.copy()复制矩阵。该函数返回矩阵的浅拷贝,不会影响原始矩阵的形状或其引用。
例如,以下脚本将新矩阵赋值给myMatrix变量并添加两列。随后使用myMatrix.copy()方法创建myCopy矩阵,并添加新行。通过自定义的debugLabel()函数在标签中显示两个矩阵的行数据:

Mine Script®
已复制
需要注意的是,矩阵的浅拷贝中的元素与原始矩阵指向相同的值。当矩阵包含特殊类型(线(line)、线填充(linefill)、方框(box)、多段线(polyline)、标签(label)、表格(table) 和 图表点(chart.point))或用户自定义类型(UDT)时,浅拷贝的元素与原始矩阵引用的是相同的对象。
以下脚本声明了一个 myMatrix 变量,并以 newLabel 作为初始值。随后通过 myMatrix.copy() 将矩阵复制到 myCopy 变量,并绘制标签数量。如下所示,图表上仅存在一个标签,因为 myCopy 中的元素与 myMatrix 中的元素引用的是同一个对象。因此,修改 myCopy 中的元素值会影响两个矩阵中的值:
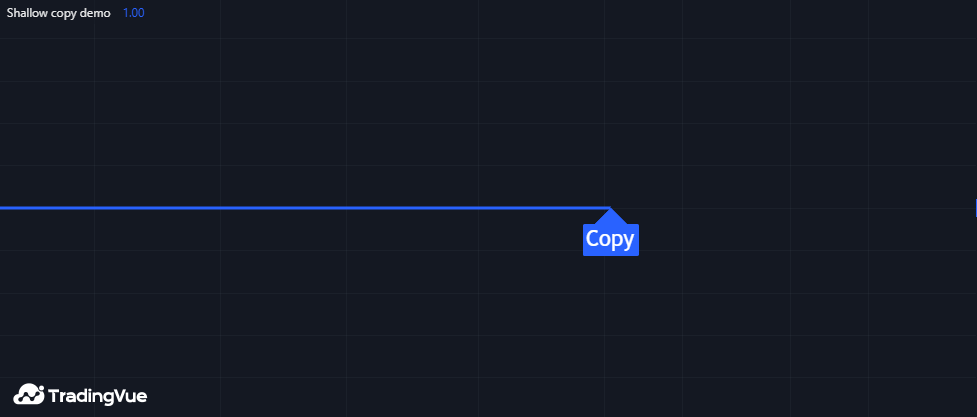
Mine Script®
已复制
深拷贝
要创建矩阵的深拷贝(即元素指向原始值副本的矩阵),需要显式复制矩阵引用的每个对象。
我们在之前的脚本中添加了自定义的 deepCopy() 方法。该方法会创建一个新矩阵,并通过嵌套 for 循环将所有元素赋值为原始对象的副本。当脚本调用此方法(而非内置的 copy())时,图表上会出现两个标签,且修改 myCopy 中的标签不会影响 myMatrix 中的标签:
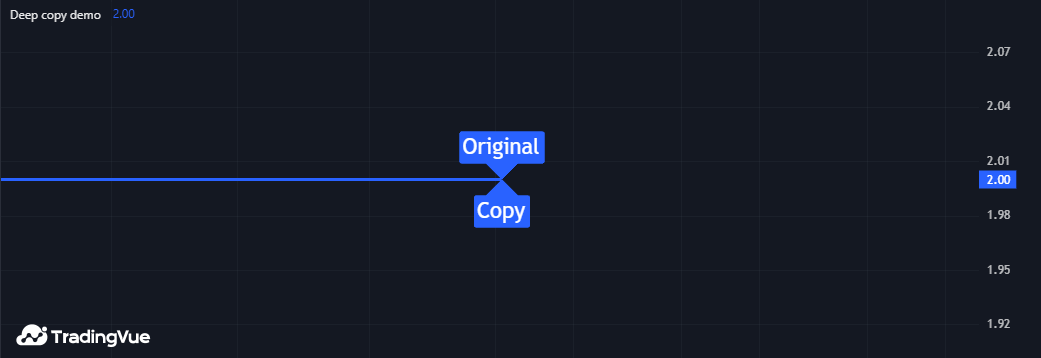
Mine Script®
已复制
子矩阵
在 Mine 语言中,子矩阵是通过 from_row/column 和 to_row/column 参数从现有矩阵浅拷贝(shallow copy)出的新矩阵,仅包含指定行列范围的数据。本质上,它是原矩阵的一个切片副本。
例如,下方脚本通过 m.submatrix() 方法从矩阵 m 创建了子矩阵 mSub,随后调用用户自定义函数 debugLabel() 在标签中显示两个矩阵的行数据:

Mine Script®
已复制
作用域与历史记录
矩阵变量会在每根K线留下历史记录,使得脚本能够使用历史引用操作符[]来访问该变量之前存储的矩阵实例。此外,脚本可以在函数、方法及条件结构的作用域内修改全局变量所引用的矩阵。
该脚本计算length根K线范围内,实体(body)和影线(wick)相对于K线波动范围(range)的平均比例,并在表格中同时显示当前数据与length根K线前的历史数据。用户自定义函数addData()将当前和历史比例数据添加至全局矩阵globalMatrix,而calcAvg()函数则通过[]操作符引用globalMatrix之前存储的previous矩阵实例,最终计算得出平均值矩阵:

Mine Script®
已复制
请注意:
addData()和calcAvg()函数不需要参数,因为它们直接与外部作用域中声明的globalMatrix和length变量交互。calcAvg()通过使用matrix.sum()相加之前的矩阵,并使用matrix.mult()将所有元素乘以1/length来计算平均值。我们将在下文的矩阵计算部分讨论这些及其他专用函数。
矩阵检测功能
矩阵形态及其元素模式的检测能力至关重要,这有助于揭示矩阵的重要特性及其与各类计算和转换的兼容性。Mine Script提供了一系列内置矩阵检测函数,包括:matrix.is_square()(检测方阵)、matrix.is_identity()(检测单位矩阵)、matrix.is_diagonal()(检测对角矩阵)、matrix.is_antidiagonal()(检测反对角矩阵)、matrix.is_symmetric()(检测对称矩阵)、matrix.is_antisymmetric()(检测反对称矩阵)、matrix.is_triangular()(检测三角矩阵)、matrix.is_stochastic()(检测随机矩阵)、matrix.is_binary()(检测二元矩阵)以及matrix.is_zero()(检测零矩阵)。
为演示这些功能,本示例包含一个自定义的inspect()方法,该方法通过结合matrix.is_*()系列函数的条件判断模块,返回矩阵的检测信息。示例将在图表标签中同时显示矩阵m的字符串表示形式以及通过m.inspect()返回的矩阵特征描述。

Mine Script®
已复制
矩阵操作
重塑矩阵
矩阵的形状决定了其与各种矩阵运算的兼容性。在某些情况下,我们需要在不改变元素数量和元素值的前提下调整矩阵的维度,这一过程称为重塑。在Mine语言中,可使用matrix.reshape()函数实现矩阵重塑。
本示例展示了矩阵多次重塑操作的结果。初始矩阵m的维度为1x8(1行8列)。通过连续调用m.reshape()方法,脚本依次将m重塑为2x4、4x2和8x1的矩阵。使用自定义的debugLabel()方法,脚本将每个重塑后的矩阵显示在图表标签中。

Mine Script®
已复制
需要注意:
- 每次调用m.reshape()时,矩阵
m中元素的顺序不会改变。 - 重塑矩阵时,行数和列数的乘积必须等于matrix.elements_count()的返回值,因为matrix.reshape()无法改变矩阵中元素的总数量。
矩阵反转
可以使用matrix.reverse()反转矩阵中所有元素的顺序。该函数将m行n列矩阵中第i行第j列元素的引用移动到第m-1-i行第n-1-j列的位置。
例如,此脚本创建一个包含1-9升序数值的3x3矩阵,然后使用reverse()方法反转其内容。通过m.debugLabel()在图表标签中显示矩阵的原始版本和修改后的版本。
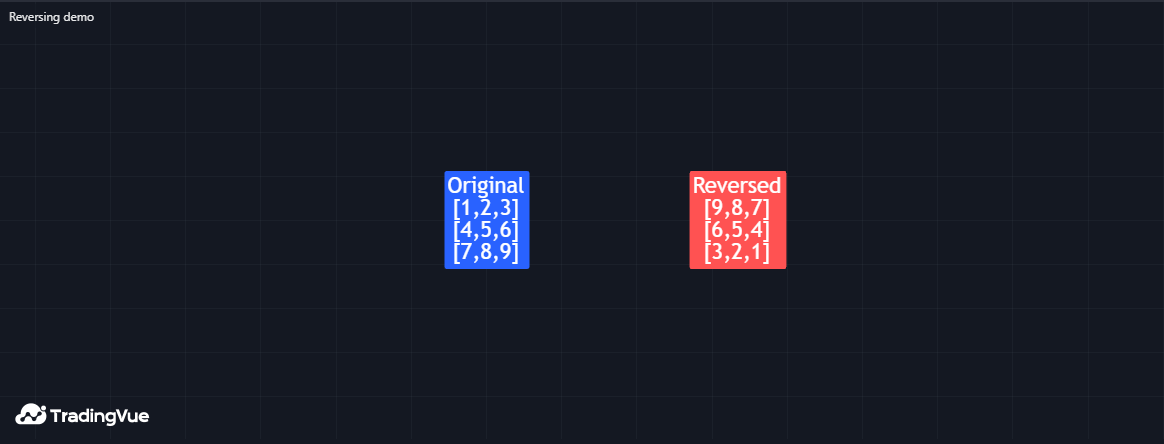
Mine Script®
已复制
矩阵转置
矩阵转置是一种基本运算,它将矩阵的所有行和列沿主对角线(行索引等于列索引的所有值组成的对角向量)进行翻转。该运算会生成一个行列维度互换的新矩阵,称为转置矩阵。脚本可以通过matrix.transpose()计算矩阵的转置。
对于任意m行n列的矩阵,matrix.transpose()返回的矩阵将具有n行m列。原矩阵中位于第i行第j列的元素,对应其转置矩阵中第j行第i列的元素。
此示例声明了一个2x4的m矩阵,使用m.transpose()方法计算其转置矩阵,并通过自定义的debugLabel()方法在图表上显示两个矩阵。如下所示,转置后的矩阵具有4x2的形状,且转置矩阵的行对应原矩阵的列。

Mine Script®
已复制
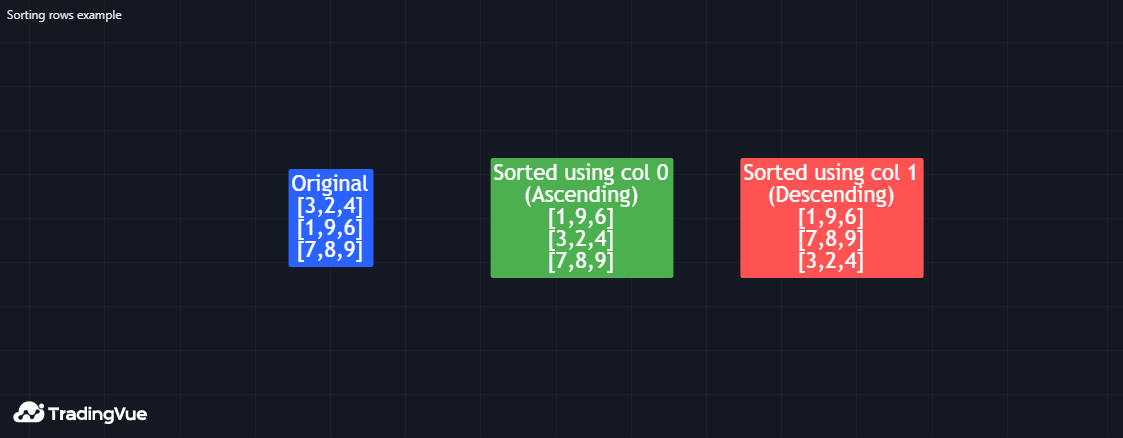
矩阵排序
脚本可以通过matrix.sort()对矩阵内容进行排序。与array.sort()(用于排序元素)不同,该函数根据指定列中的值(默认为order.ascending)重新排列矩阵中的所有行。
此脚本声明了一个3x3的m矩阵,将m1副本的行按第一列升序排序,将m2副本的行按第二列降序排序,并使用我们的debugLabel()方法在标签中显示原始矩阵和排序后的副本。
Mine Script®
已复制
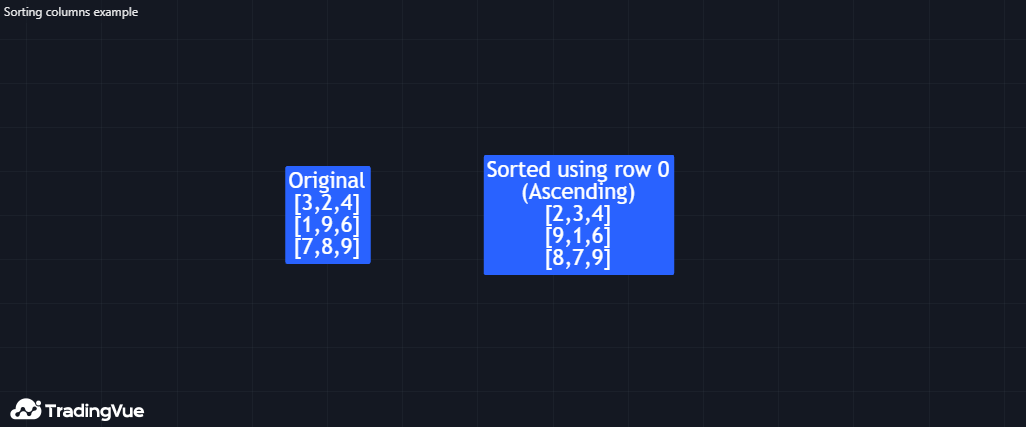
需要注意的是,matrix.sort() 不会对矩阵的列进行排序。但可以借助 matrix.transpose() 函数来实现这一功能。
例如,本脚本包含一个 sortColumns() 方法,该方法使用 sort() 方法对矩阵转置进行排序,排序依据为原矩阵行对应的列值。该脚本使用此方法,基于矩阵 m 第一行的内容对矩阵进行排序。
Mine Script®
已复制
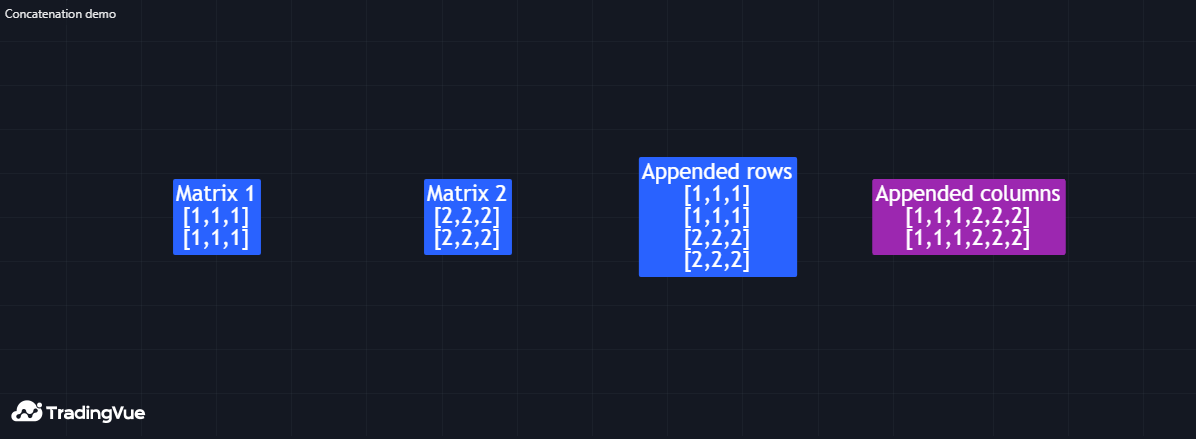
矩阵拼接
脚本可以使用matrix.concat()拼接两个矩阵。该函数将id2矩阵的行追加到具有相同列数的id1矩阵末尾。
若要创建一个矩阵,使其元素表示将一个矩阵的列追加到另一个矩阵之后,需执行以下操作:
- 对两个矩阵进行转置
- 在转置后的矩阵上使用matrix.concat()
- 对结果再次转置
例如,本脚本将m2矩阵的行追加到m1矩阵之后,并通过矩阵转置实现列的拼接。使用自定义debugLabel()方法在标签中显示m1和m2矩阵,以及它们行拼接和列拼接后的结果。
Mine Script®
已复制
矩阵计算
元素级运算
Mine脚本可通过matrix.avg()、matrix.min()、matrix.max()和matrix.mode()计算矩阵内所有元素的平均值、最小值、最大值和众数。这些函数的操作方式与其对应的array.*函数相同,允许用户使用相同的语法对矩阵、其子矩阵及其行和列执行元素级计算。例如,在值为1-9的3x3矩阵和包含相同9个元素的数组上调用内置的*.avg()函数,两者都将返回值5。
下方脚本使用*.avg()、*.max()和*.min()方法计算周期内OHLC数据的发展中平均值和极值。当queueColumn为true时,它会在ohlcData矩阵末尾添加一列开盘价、最高价、最低价和收盘价数值。当为false时,脚本使用get()和set()矩阵方法调整最后一列中的元素以反映当前周期的发展中HLC值。该脚本使用ohlcData矩阵、submatrix()以及row()和col()数组来计算length周期内发展中的OHLC4和HL2平均值,length周期内的最高价最大值和最低价最小值,以及当前周期发展中的OHLC4价格。
Mine Script®
已复制
需要注意的是:
- 在此示例中,我们交替使用了
array.*()和matrix.*()方法,以展示它们在语法和行为上的相似性。 - 用户可以通过将matrix.avg()乘以matrix.elements_count()来计算与array.sum()等效的矩阵求和结果。
特殊计算
Mine Script提供多个内置函数用于执行基础矩阵运算和线性代数操作,包括:matrix.sum()(矩阵求和)、matrix.diff()(矩阵差分)、matrix.mult()(矩阵乘法)、matrix.pow()(矩阵幂运算)、matrix.det()(行列式计算)、matrix.inv()(矩阵求逆)、matrix.pinv()(伪逆矩阵)、matrix.rank()(矩阵秩)、matrix.trace()(矩阵迹)、matrix.eigenvalues()(特征值计算)、matrix.eigenvectors()(特征向量计算)以及matrix.kron()(克罗内克积)。这些高级功能支持各类矩阵计算与变换。
下文将通过基础示例说明几个核心函数的使用方法。
matrix.sum() 和 matrix.diff()
脚本可以通过matrix.sum()和matrix.diff()函数对两个相同维度的矩阵,或者矩阵与标量值进行加法和减法运算。这些函数使用id2矩阵或标量值来对id1矩阵中的元素进行加法或减法操作。
这个脚本展示了Mine中进行矩阵加减法的简单示例:它创建一个3x3矩阵,计算其转置矩阵,然后计算这两个矩阵的matrix.sum()和matrix.diff()结果。该示例在图表标签中显示原始矩阵、转置矩阵以及求和与求差的结果矩阵。
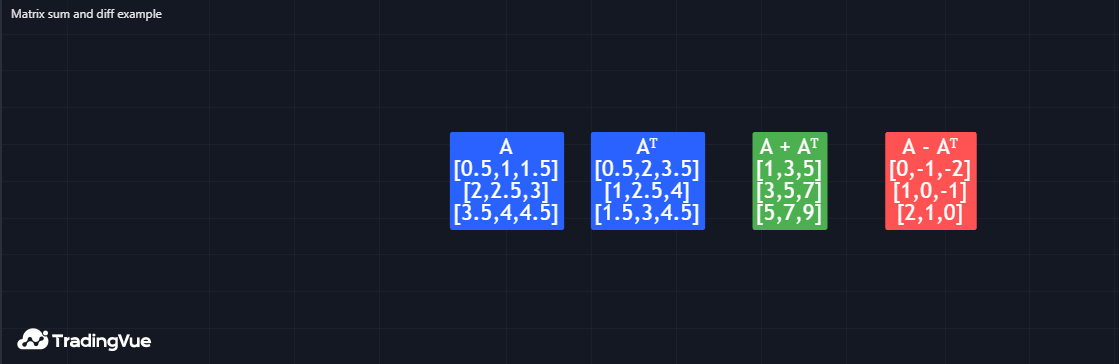
Mine Script®
已复制
需要注意的是:
- 在本示例中,我们将原始矩阵标记为"A",转置矩阵标记为"Aᵀ"。
- 将"A"与"Aᵀ"相加会生成一个对称矩阵,而将它们相减则会生成一个反对称矩阵。
matrix.mult()
脚本可通过matrix.mult()函数实现矩阵乘法运算,该函数同样支持矩阵与数组或标量值的乘法操作。
在进行两个矩阵相乘时,与加减法不同,矩阵乘法不要求两个矩阵维度相同,但第一个矩阵的列数必须等于第二个矩阵的行数。matrix.mult()返回的结果矩阵将保留第一个矩阵的行数和第二个矩阵的列数。例如:一个2×3矩阵与3×4矩阵相乘,将生成一个2行4列的矩阵(如下所示)。结果矩阵中的每个值都是第一个矩阵(id1)对应行与第二个矩阵(id2)对应列的点积结果:

Mine Script®
已复制
需要注意的是:
- 与标量乘法不同,矩阵乘法不满足交换律,即
matrix.mult(a, b)产生的结果不一定与matrix.mult(b, a)相同。在我们的示例中,后者会引发运行时错误,因为矩阵b的列数与矩阵a的行数不相等。
当进行矩阵与数组的乘法运算时,该函数将操作视为矩阵与单列矩阵相乘,但会返回一个数组(其元素数量与矩阵id1的行数相同)。若matrix.mult()的id2参数为标量值,则该函数会返回一个新矩阵,其每个元素都是矩阵id1对应元素与该标量值的乘积结果。
matrix.det()
行列式是与方阵相关联的标量值,用于描述矩阵的某些特性,特别是其可逆性。若矩阵存在逆矩阵,则其行列式值非零;反之,该矩阵为奇异矩阵(不可逆)。脚本可通过matrix.det()计算矩阵的行列式。
开发者可运用行列式实现以下功能:
- 检测矩阵间的相似性
- 判别满秩矩阵与秩亏矩阵
- 求解线性方程组等应用场景
例如,本脚本利用行列式配合克莱姆法则,求解未知量数目匹配的线性方程组。用户自定义的solve()函数返回包含方程组各未知量解的数组,其中第n个元素为:用常数列替换系数矩阵第n列后的行列式值,除以原系数矩阵行列式值。
脚本中定义的矩阵m存储了以下三个方程的系数和常数项:
3 * x0 + 4 * x1 - 1 * x2 = 8
5 * x0 - 2 * x1 + 1 * x2 = 4
2 * x0 - 2 * x1 + 1 * x2 = 1该方程组的解为(x₀=1, x₁=2, x₂=3)。脚本通过m.solve()方法从矩阵m计算出这些解值,并将结果绘制在图表上:
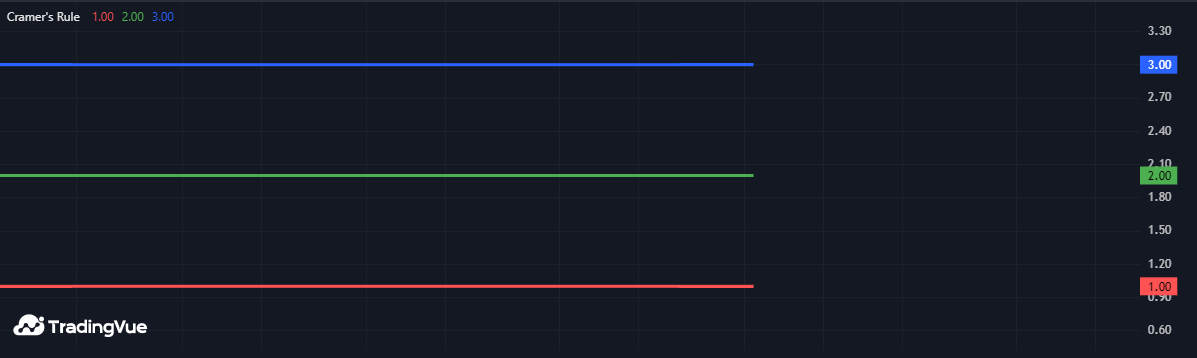
Mine Script®
已复制
需要注意的是:
- 方程组的求解在回归分析中尤为重要,例如线性回归和多项式回归分析
- 克莱姆法则适用于小型方程组求解,但在处理大型方程组时计算效率较低。对于此类情况,通常更推荐采用高斯消元法等替代算法
matrix.inv() 和 matrix.pinv()
对于任意非奇异方阵,都存在一个逆矩阵,当它与原矩阵相乘时会产生单位矩阵。逆矩阵在多种矩阵变换和方程组求解中具有实用价值。脚本可以通过matrix.inv()函数计算存在的矩阵逆。
对于奇异(不可逆)矩阵,无论矩阵是否为方阵或行列式是否非零<_PageMatrices_MatrixCalculations_SpecialCalculations_MatrixDet>,都可以通过matrix.pinv()函数计算其广义逆(伪逆)。需要注意的是,与真逆不同,伪逆与原矩阵的乘积不一定等于单位矩阵,除非原矩阵是可逆的。
以下示例根据用户输入构建一个2x2的m矩阵,然后使用m.inv()和m.pinv()方法计算m的逆矩阵或伪逆。脚本在图表标签中显示原始矩阵、其逆矩阵或伪逆以及它们的乘积结果:

Mine Script®
已复制
需要注意的是:
matrix.rank()
矩阵秩表示矩阵所包含的线性无关向量(行或列)的数量。本质上,矩阵秩衡量的是无法表示为其他向量线性组合的向量数量,或者说包含独特信息的向量数量。脚本可以通过matrix.rank()计算矩阵的秩。
该脚本检测两个3x3矩阵(m1和m2)中线性无关向量的数量,并将这些值绘制在独立面板中。如图表所示,m1.rank()的值为3,因为每个向量都是唯一的;而m2.rank()的值为1,因为它只有一个独特向量:
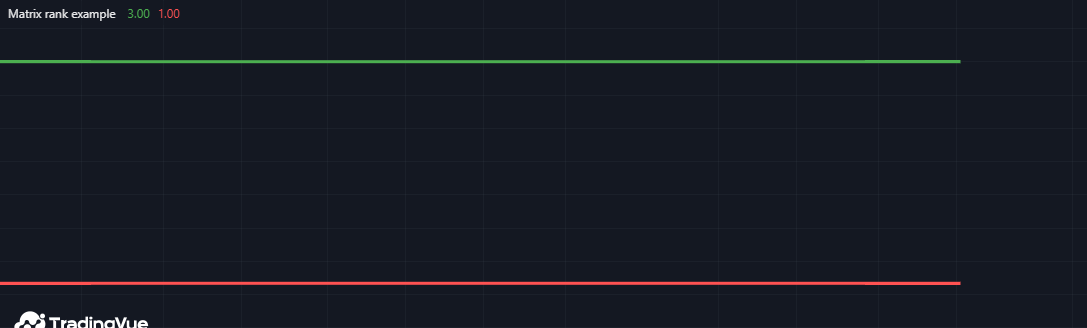
Mine Script®
已复制
需要注意的是:
- 矩阵可能达到的最大秩值是其行数和列数中的较小值。具有最大可能秩的矩阵称为满秩矩阵,任何非满秩的矩阵都称为秩亏矩阵。
- 满秩方阵的行列式非零,且这类矩阵存在逆矩阵。反之,秩亏矩阵的行列式始终为0。
- 对于所有元素值都相同的矩阵(如全0矩阵),其秩始终为0,因为没有任何向量包含独特信息。而对于包含不同数值的其他矩阵,最小可能秩为1。
错误处理
除了由于语法不当在脚本编译期间出现的常规编译错误外,使用矩阵的脚本在执行过程中还可能引发特定的运行时错误。当脚本引发运行时错误时,会在脚本标题旁显示红色感叹号图标。用户可通过点击该图标查看错误信息。
本节将讨论用户在使用矩阵时可能遇到的运行时错误。
行/列索引(xx)超出范围,矩阵行/列尺寸为(yy)
该运行时错误发生在尝试使用matrix.get()、matrix.set()、matrix.fill()和matrix.submatrix()等函数访问超出矩阵维度的索引时,也包括一些涉及矩阵行列操作的函数。
例如,以下代码包含两行会产生此运行时错误的语句:m.set()方法引用了一个不存在的行索引(2);m.submatrix()方法引用的列索引范围包含to_column-1,当to_column值为4时会导致运行时错误,因为引用的最后一个列索引(3)在矩阵m中不存在:
Mine Script®
已复制
用户可通过确保函数调用不引用大于或等于矩阵行数/列数的索引值,来避免脚本中出现此类错误。
数组大小与矩阵行数/列数不匹配
使用matrix.add_row()和matrix.add_col()函数向非空矩阵插入行列时,插入数组的维度必须与矩阵规格相符:
- 新增行的数组长度必须匹配矩阵列数
- 新增列的数组长度必须匹配矩阵行数
若维度不符,脚本将抛出此运行时错误。例如:
Mine Script®
已复制
需要注意的是:
- 当矩阵
m为空时,可以插入任意大小的行或列数组,如第一个m.add_col()语句所示。
无法在矩阵ID为na时调用矩阵方法
当矩阵变量被赋值为na时,表示该变量未引用任何现有矩阵对象。因此,无法对其使用内置的matrix.*()函数和方法。例如:
Mine Script®
已复制
要解决此错误,请在使用 matrix.*() 函数前先将 m 赋值为一个有效的矩阵实例。
矩阵尺寸过大。矩阵的最大元素数量限制为100,000个。
无论矩阵的形状如何,其元素总数(matrix.elements_count())都不得超过100,000个。例如,以下脚本会报错,因为它向矩阵m中插入了1000行,每行包含101个元素(总元素数达101,000个,超出限制):
Mine Script®
已复制
行/列索引必须满足 0 ≤ from_row/column < to_row/column 的条件。
当使用带有 from_row/column 和 to_row/column 索引的 matrix.*() 函数时,from_ 值必须小于对应的 to_* 值,且最小可能值为 0。否则,脚本将引发运行时错误。
例如,以下脚本尝试从一个 4×4 的 m 矩阵声明子矩阵时,将 from_row 值设为 2 且 to_row 值设为 2,这将导致错误:
Mine Script®
已复制
矩阵id1和id2必须具有相同的行数和列数才能进行加法运算。
使用matrix.sum()和matrix.diff()函数时,id1和id2矩阵必须满足:
- 行数相同
- 列数相同
若尝试对维度不匹配的矩阵进行加减运算,将触发错误(如下列代码所示):
Mine Script®
已复制
矩阵id1的列数必须等于矩阵(或数组元素数量)id2的行数。
使用matrix.mult()进行矩阵乘法运算时,必须满足:
- 矩阵
id2的行数(matrix.rows()) - 或数组
id2的元素数(array.size()) - 必须等于矩阵
id1的列数(matrix.columns())
维度不匹配时将触发错误。例如,以下脚本尝试对两个2×3矩阵进行乘法运算(虽然这两个矩阵可以相加,但不能相乘):
Mine Script®
已复制
该运算不适用于非方阵。
部分矩阵运算(包括matrix.inv()求逆、matrix.det()行列式计算、matrix.eigenvalues()特征值求解和matrix.eigenvectors()特征向量求解)仅适用于行数与列数相同的方阵。若对非方阵执行这些运算,系统将报错提示"运算不可用"或"无法为矩阵id计算结果"。例如:
Mine Script®
已复制